<!DOCTYPE html>
<html>
<head>
<style>
.mermaid {
background-color: #fff;
border: 1px solid #ddd;
padding: 10px;
border-radius: 5px;
}
</style>
</head>
<body>

Hello world

[TOC]

VScode语法

打开终端 ctrl+ˋ

Markdown语法

纯粹的 Markdown 语法其实非常简单, 70 行的语法介绍就可以写完.


# 一级标题

## 二级标题

### 三级标题

每写完一个段落要隔一行空行.

就像这样, 隔了一行空行.

---

分割线

**重点加粗**

*斜体*

~~删除线~~

---

列表:

* 无序列表
  * demo
  
  * 嵌套无序列表
  * 嵌套无序列表
* 无序列表
* 无序列表

1. 有序列表 1
   1. 嵌套有序列表 1
   2. 嵌套有序列表 2
2. 有序列表 2
3. 有序列表 3

---

引用文本:

> 就这样引用别人的话
> 沃兹基硕德
> By. MoFrom_FG

---

这是 `行内代码` 语法.

代码块语法:

''' python
print("Hello, World!")
'''

请将 **'** 替换成 **`**.



---

[百度超链接测试](www.baidu.com)

![图片提示语](/FG.jpg)

---

表格:

| 表头 | 表头 |
| ---- | ---- |
| 内容 | 内容 |
| 内容 | 内容 |

---

注释:

<!-- 你看不见我 -->

#标题

一级标题

二级标题

三级标题

段落.

#段落


段落与段落之间要空一行

像这样

#分割线

用大于等于3的横线表示分割线
注意：要在段落后空一行，否则会变成标题

加粗,斜体和删除线

做笔记的时候, 我们常常会有这样的要求, "加粗, 斜体和删除线", 作为笔记的标记

**重点加粗**

*斜体*

~~删除线~~

~~删除线~~

<u>下划线</u>

重点加粗

斜体

~~删除线~~

$\underline{下划线}$

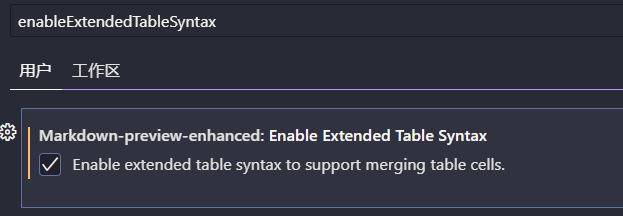
Markdown Preview Enhanced 拓展功能

==高亮==

==高亮==

快捷键

选中文本之后, 按下 Ctrl + B 可以给选中文本加粗.
同理 Ctrl + I 可以让选中文本变为斜体.
要进行缩进 (书写嵌套列表), 你可以使用 VS Code 的快捷键 Ctrl + [ 和 Ctrl + ].

这个快捷键可以将代码向左或向右进行缩进!

列表

列表是记笔记时非常基本的元素, 在 Markdown 中, 可以用很方便的格式书写列表:

* 无序列表
  * 嵌套无序列表
  * 嵌套无序列表
* 无序列表
* 无序列表

1. 有序列表 1
   1. 嵌套有序列表 1
   2. 嵌套有序列表 2
2. 有序列表 2
3. 有序列表 3

无序列表
- 嵌套无序列表
- 嵌套无序列表
无序列表
无序列表

有序列表 1
1. 嵌套有序列表 1
2. 嵌套有序列表 2
有序列表 2
有序列表 3

Markdown Preview Enhanced 拓展功能

任务列表:

- [x] 已经完成的事 1
- [x] 已经完成的事 2
- [x] 已经完成的事 3
- [ ] 仍未完成的事 4
- [ ] 仍未完成的事 5

任务列表:

[x] 已经完成的事 1
[x] 已经完成的事 2
[x] 已经完成的事 3
[ ] 仍未完成的事 4
[ ] 仍未完成的事 5

引用和代码

引用文本:

> 就这样引用别人的话
> 沃兹基硕德
> By. MoFrom_FG

这是 `行内代码` 语法.

代码块语法:

''' python
print("Hello, World!")
'''

==注意要将 ' 替换成 `.==

引用文本:

就这样引用别人的话
沃兹基硕德
By. MoFromFG

这是 行内代码 语法.

代码块语法:

print("Hello, World!")

==注意要将 ' 替换成 `.==

Markdown Preview Enhanced 拓展功能

代码行数的显示:

''' javascript {.line-numbers}
function add(x, y) {
  return x + y
}
'''

注意要将 ' 替换成 `.

代码行数的显示:

function add(x, y) {
  return x + y
}

注意要将 ' 替换成 `.

超链接和图片

可以用下面的语法插入超链接和图片:

[超链接名称](链接地址)

![图片提示语](图片地址)

例如, 可以使用网址和图床:

[MoFrom's Blog](https://mofromfg.top/)

![Article's IMG](https://mofromfg.top/images/FG.jpg)

也可以在本地用相对地址:

[Other](other.md)

![Article's IMG](/FG.jpg)

MoFrom_FG's Blog

在本地用相对地址:

Other

剪贴板图片插入

按下 Ctrl + , , 打开设置窗口, 输入 Paste Image Path 并搜索, 将框内的文本改成 ${currentFileDir}/images.
按下快捷键 ctrl + alt + P

表格

可以很方便的在做笔记的时候加入表格

表格:

| 表头 | 表头 |
| ---- | ---- |
| 内容 | 内容 |
| 内容 | 内容 |

表格:

表头	表头
内容	内容
内容	内容

扩展功能

拓展语法:

| 表头 | 表头 |
| ---- | ---- |
| 内容 | 内容 |
| >    | 内容 |

| 表头 | 表头 |
| ---- | ---- |
| 内容 | 内容 |
| ^    | 内容 |

拓展语法:

表头	表头
内容	内容
>	内容

表头	表头
内容	内容
^	内容

表格自动对齐Shift + Alt + F

注释

注释不会被渲染出来.
可以随手做点草稿, 如果还想保留着, 但是不显示, 就可以按下快捷键 Ctrl + \ 将当前行注释 / 反注释.

注释:

<!-- 你看不见我 -->

<!-- 多行注释
就像这样 -->

注释:

有一点很重要的就是, VS Code 会在你每次修改代码之后, 重新渲染一遍.
如果有很多很多的数学公式, 渲染会很慢, 这时候有两个建议:

分成多个文件, 避免单文件过大!
将你暂时不看的部分注释掉, 加快渲染速度!

数学公式支持

Markdown 的数学公式吸纳了大部分的 Latex 语法, 你可以以一种简单的方式在 VS Code 中书写数学公式.

行内公式: 

单位圆 $x^2+y^2=1$

公式块:

$$
\begin{cases}
x=\rho\cos\theta \\
y=\rho\sin\theta \\
\end{cases}
$$

行内公式:

单位圆 $x^2+y^2=1$

公式块:

$$
\begin{cases}
x=\rho\cos\theta \
y=\rho\sin\theta \
\end{cases}
$$

VS Code 有着非常便捷好用的自动补全功能, 只需要简单地打出你想打的内容的几个字母 (乱序也行), 再使用 ↑ ↓ 进行选择, 最后按下回车就可以打出你想要的内容.

再使用 HyperSnips 插件, 就能够写得飞快.

1.上标和下标

上标 $x^2 + y^{12} = 1$

上标 $x_1 + y_{12} = 1$

上标 $x^2 + y^{12} = 1$

上标 $x_1 + y_{12} = 1$

HyperSnips自动扩展

xsr  =>  x^{2}

xtp  =>  x^{...}

x1  =>  x_1

xii  =>  x_i

xsb  =>  x_{...}

2.分式

较小的行内行分数 $\frac{1}{2}$

展示型的分式 $\displaystyle\frac{x+1}{x-1}$

较小的行内行分数 $\frac{1}{2}$

展示型的分式 $\displaystyle\frac{x+1}{x-1}$

其中 \displaystyle 用于将行内展示转为块状展示.

HyperSnips自动扩展

1/  =>  \frac{1}{...}

(1 + 2)/  =>  \frac{(1+2)}{...}

//  =>  \frac{...}{...}

3.根式

开平方 $\sqrt{2}$

开 $n$ 次方 $\sqrt[n]{2}$

开平方 $\sqrt{2}$

开 $n$ 次方 $\sqrt[n]{2}$

HyperSnips自动扩展

hsq  =>  \sqrt{...}

4.空格

数学公式中的空格和换行都会在编译时被忽略，想要实现「空格」的效果，需要用特别的命令。

紧贴 $a\!b$

没有空格 $ab$

小空格 $a\,b$

中等空格 $a\;b$

大空格 $a\ b$

quad 空格 $a\quad b$

两个 quad 空格 $a\qquad b$

紧贴 $a!b$

没有空格 $ab$

小空格 $a,b$

中等空格 $a;b$

大空格 $a\ b$

quad 空格 $a\quad b$

两个 quad 空格 $a\qquad b$

5.累加累乘和积分

累加 $\sum_{k=1}^n\frac{1}{k}  \quad  \displaystyle\sum_{k=1}^n\frac{1}{k}$

累乘 $\prod_{k=1}^n\frac{1}{k}  \quad  \displaystyle\prod_{k=1}^n\frac{1}{k}$

积分 $\displaystyle \int_0^1x{\rm d}x  \quad  \iint_{D_{xy}}  \quad  \iiint_{\Omega_{xyz}}$

累加 $\sum_{k=1}^n\frac{1}{k} \quad \displaystyle\sum_{k=1}^n\frac{1}{k}$

累乘 $\prod_{k=1}^n\frac{1}{k} \quad \displaystyle\prod_{k=1}^n\frac{1}{k}$

积分 $\displaystyle \int_0^1x{\rm d}x \quad \iint_{D_{xy}} \quad \iiint_{\Omega_{xyz}}$

HyperSnips自动扩展

sum  =>  \sum_{...}

prod  =>  \prod_{<n=1>}^{<\infty>} ...

int  =>  \int

dint  =>  \int_{<-\infty>}^{<\infty>} ... \mathrm{d}x

6.括号修饰

用 \left 和 \right 可以让括号适配内部大小

圆括号 $\displaystyle \left(\sum_{k=1}^{n}\frac{1}{k} \right)^2$

方括号 $\displaystyle \left[\sum_{k=1}^{n}\frac{1}{k} \right]^2$

花括号 $\displaystyle \left\{\sum_{k=1}^{n}\frac{1}{k} \right\}^2$

尖括号 $\displaystyle \left\langle\sum_{k=1}^{n}\frac{1}{k} \right\rangle^2$

圆括号 $\displaystyle \left(\sum_{k=1}^{n}\frac{1}{k} \right)^2$

方括号 $\displaystyle \left[\sum_{k=1}^{n}\frac{1}{k} \right]^2$

花括号 $\displaystyle \left{\sum_{k=1}^{n}\frac{1}{k} \right}^2$

尖括号 $\displaystyle \left\langle\sum_{k=1}^{n}\frac{1}{k} \right\rangle^2$

HyperSnips自动扩展

@(  =>  \left( ... \right)

@[  =>  \left[ ... \right]

@{  =>  \left\{ ... \right\}

@<  =>  \left< ... \right>

set  =>  \{ ... \}

7.多行算式对齐

居中:

$$
\begin{aligned}
y &=(x+5)^2-(x+1)^2 \\
&=(x^2+10x+25)-(x^2+2x+1) \\
&=8x+24 \\
\end{aligned}
$$

左对齐:

$
\begin{aligned}
y &=(x+5)^2-(x+1)^2 \\
&=(x^2+10x+25)-(x^2+2x+1) \\
&=8x+24 \\
\end{aligned}
$

居中:

$$
\begin{aligned}
y &=(x+5)^2-(x+1)^2 \
&=(x^2+10x+25)-(x^2+2x+1) \
&=8x+24 \
\end{aligned}
$$

左对齐:

$\begin{aligned}
y &=(x+5)^2-(x+1)^2 \
&=(x^2+10x+25)-(x^2+2x+1) \
&=8x+24 \
\end{aligned}$

HyperSnips自动扩展

ali  =>
\begin{aligned}
... \\
\end{aligned}

8.方程组

$$
\begin{cases}
k_{11}x_1+k_{12}x_2+\cdots+k_{1n}x_n=b_1 \\
k_{21}x_1+k_{22}x_2+\cdots+k_{2n}x_n=b_2 \\
\cdots \\
k_{n1}x_1+k_{n2}x_2+\cdots+k_{nn}x_n=b_n \\
\end{cases}
$$

$$
\begin{cases}
k_{11}x_1+k_{12}x_2+\cdots+k_{1n}x_n=b_1 \
k_{21}x_1+k_{22}x_2+\cdots+k_{2n}x_n=b_2 \
\cdots \
k_{n1}x_1+k_{n2}x_2+\cdots+k_{nn}x_n=b_n \
\end{cases}
$$

HyperSnips自动扩展

case  =>
\begin{cases}
... \\
\end{cases}

9.矩阵

矩阵:

$$
\begin{pmatrix}
1 & 1 & \cdots & 1 \\
1 & 1 & \cdots & 1 \\
\vdots & \vdots & \ddots & \vdots \\
1 & 1 & \cdots & 1 \\
\end{pmatrix}

\quad

\begin{bmatrix}
1 & 1 & \cdots & 1 \\
1 & 1 & \cdots & 1 \\
\vdots & \vdots & \ddots & \vdots \\
1 & 1 & \cdots & 1 \\
\end{bmatrix}
$$ 

行列式: 

$$
\begin{vmatrix}
1 & 1 & \cdots & 1 \\
1 & 1 & \cdots & 1 \\
\vdots & \vdots & \ddots & \vdots \\
1 & 1 & \cdots & 1 \\
\end{vmatrix}
$$

矩阵:

$$
\begin{pmatrix}
1 & 1 & \cdots & 1 \
1 & 1 & \cdots & 1 \
\vdots & \vdots & \ddots & \vdots \
1 & 1 & \cdots & 1 \
\end{pmatrix}
$$
$$
\begin{bmatrix}
1 & 1 & \cdots & 1 \
1 & 1 & \cdots & 1 \
\vdots & \vdots & \ddots & \vdots \
1 & 1 & \cdots & 1 \
\end{bmatrix}
$$

行列式:

$$
\begin{vmatrix}
1 & 1 & \cdots & 1 \
1 & 1 & \cdots & 1 \
\vdots & \vdots & \ddots & \vdots \
1 & 1 & \cdots & 1 \
\end{vmatrix}
$$

HyperSnips自动扩展

bmat2  =>  \begin{bmatrix} ... & ... \\ ... & ... \\\end{bmatrix}

vec2  =>  \begin{pmatrix} ... \\ ... \\\end{pmatrix}

10.特殊字符

HyperSnips自动扩展

alpha  =>  \alpha

Sigma  =>  \Sigma

11.公式编号与引用

$$
x+2 \tag{1.2}
$$

$$
\begin{equation}
x^n+y^n=z^n
\end{equation}
$$

由公式 $(1.2)$ 可得到结论

$$
x+2 \tag{1.2}
$$

$$
\begin{equation}
x^n+y^n=z^n
\end{equation}
$$

由公式 $(1.2)$ 可得到结论

12.零碎的用法

点乘 $\cdot$, 叉乘 $\times$, 异或 $\otimes$, 直和 $\oplus$, 加减 $\pm$, 复合 $\circ$.
小于等于 $\leq$, 大于等于 $\geq$, 不等 $\neq$, 恒等 $\equiv$, 约等 $\approx$, 等价 $\cong$, 相似 $\sim$, 相似等于 $\simeq$, 点等 $\doteq$.
逻辑与 $\land$, 逻辑或 $\lor$, 逻辑非 $\lnot$, 蕴涵 $\to$, 等价 $\leftrightarrow$.
因为 $\because$, 所以 $\therefore$, 存在 $\exist$, 任意 $\forall$.
左小箭头 $\leftarrow$, 右小箭头 $\rightarrow$, 左大箭头 $\Leftarrow$, 右大箭头 $\Rightarrow$, 右长箭头 $\xrightarrow[fgh]{abcde}$.
属于 $\in$, 包含于 $\subset$, 真包含于 $\subseteq$, 交 $\cap$, 并 $\cup$, 空集 $\empty$
短向量 $\vec{x}$, 长向量 $\overrightarrow{AB}$, 上横线 $\overline{p}$.
无限 $\infty$, 极限 $\lim$, 微分 ${\rm d}$, 偏导 $\partial$, 点求导 $\dot{y}$, 点二阶导 $\ddot{y}$, 变化量 $\Delta$, 梯度 $\nabla$.
横省略 $\cdots$, 竖省略 $\vdots$, 斜省略 $\ddots$.
常见函数 $\sin$, $\cos$, $\tan$, $\arcsin$, $\arccos$, $\arctan$, $\ln$, $\log$, $\exp$.

点乘 $\cdot$, 叉乘 $\times$, 异或 $\otimes$, 直和 $\oplus$, 加减 $\pm$, 复合 $\circ$.
小于等于 $\leq$, 大于等于 $\geq$,小于$\lt$,大于$\gt$, 不等 $\neq$, 恒等 $\equiv$, 约等 $\approx$, 等价 $\cong$, 相似 $\sim$, 相似等于 $\simeq$, 点等 $\doteq$.
逻辑与 $\land$, 逻辑或 $\lor$, 逻辑非 $\lnot$, 蕴涵 $\to$, 等价 $\leftrightarrow$.
因为 $\because$, 所以 $\therefore$, 存在 $\exist$, 任意 $\forall$.
左小箭头 $\leftarrow$, 右小箭头 $\rightarrow$, 左大箭头 $\Leftarrow$, 右大箭头 $\Rightarrow$, 右长箭头 $\xrightarrow[fgh]{abcde}$.
属于 $\in$, 包含于 $\subset$, 真包含于 $\subseteq$, 交 $\cap$, 并 $\cup$, 空集 $\empty$
短向量 $\vec{x}$, 长向量 $\overrightarrow{AB}$, 上横线 $\overline{p}$, 上波浪线 $\widetilde{x}$
无限 $\infty$, 极限 $\lim$, 微分 ${\rm d}$, 偏导 $\partial$, 点求导 $\dot{y}$, 点二阶导 $\ddot{y}$, 变化量 $\Delta$, 梯度 $\nabla$.
横省略 $\cdots$, 竖省略 $\vdots$, 斜省略 $\ddots$.
常见函数 $\sin$, $\cos$, $\tan$, $\arcsin$, $\arccos$, $\arctan$, $\ln$, $\log$, $\exp$.

HyperSnips自动扩展

**  =>  \cdot
xx  =>  \times
otimes  =>  \otimes
<=  =>  \le
!=  =>  \neq
==  =>  \equiv
~~  =>  \thickapprox
sim  =>  \sim
land  =>  \land
lor  =>  \lor
bec  =>  \because
thr  =>  \therefore
EE  =>  \exists
AA  =>  \forall
inn  =>  \in
sse  =>  \subseteq
sqs  =>  \sqsubseteq
cap  =>  \cap
cup  =>  \cup
empty  =>  \empty
oo  =>  \infty
lim  =>  \lim_{<n> \to <\infty>}
dd  =>  \mathrm{d}
part  =>  \frac{\partial <V>}{\partial <x>}
Delta  =>  \Delta
nabla  =>  \nabla
...  =>  \cdots
sin  =>  \sin
还有特别重要的数集、向量、矩阵符号：

RR  =>  \mathbb{R}
NN  =>   \mathbb{N}
txt  =>  \text{...}
xbar  =>  \bar{x}
xhat  =>  \hat{x}
xhvec  =>  \vec{x}
xhdot  =>  \dot{x}
Xbb  =>  \mathbb{X}
Xbs  =>  \boldsymbol{X}
Xbm  =>  \bm{X}
Xbf  =>  \mathbf{X}
Xsf  =>  \mathsf{X}
Xcal  =>  \mathcal{X}
Xfrak  =>  \mathfrak{X}
Xrm  =>  \mathrm{X}

13.流程图教程

此处使用mermaid进行画图，这里的例子是关于流程图的一些知识点，是在vscode + Markdown Preview Enhanced（插件）来做的。如果想进行实验，可以使用此组合来尝试一下。

流程图由结点（图形类别，比如菱形、圆形等）和边（箭头、直线、点线）、子图等组成。

结点类型

ˋˋˋmermaid
%% graph TD; comment
graph LR

Zero

A(This is A)

B[This is B]

C([This is C])

D[[This is D]]

E[(Database E)]

F((This is F))

G>This is G]

H{This is H}

I{{This is I}}

J[/J/]

K[\K\]

L[/L\]

M[\ M/]

Zero --> A --> B --> C --> D --> E --> F --> G --> H --> I --> J --> K --> L --> M
ˋˋˋ

显示如下：

%% graph TD; comment
graph LR

Zero

A(This is A)

B[This is B]

C([This is C])

D[[This is D]]

E[(Database E)]

F((This is F))

G>This is G]

H{This is H}

I{{This is I}}

J[/J/]

K[\K\]

L[/L\]

M[\ M/]

Zero --> A --> B --> C --> D --> E --> F --> G --> H --> I --> J --> K --> L --> M

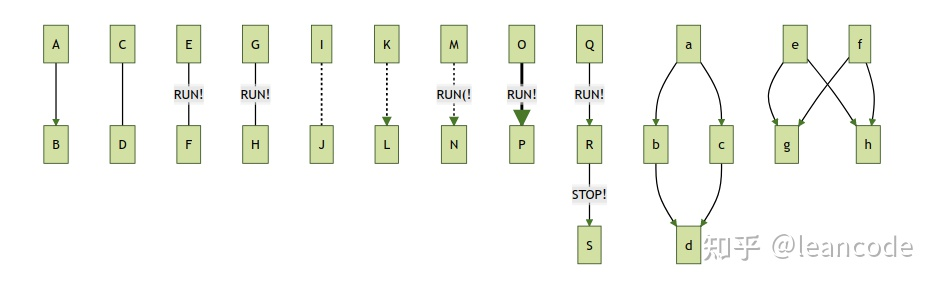
连接线类型


ˋˋˋmermaid
graph TD

A-->B
C---D
E--RUN!---F
G---|RUN!|H
I -.- J
K .-> L
M -."RUN(!".->N
O ==RUN!==>P
Q --RUN!-->R--STOP!-->S

a --> b & c--> d
e & f--> g & h
ˋˋˋ

显示如下:

graph TD

A-->B
C---D
E--RUN!---F
G---|RUN!|H
I -.- J
K .-> L
M -."RUN(!".->N
O ==RUN!==>P
Q --RUN!-->R--STOP!-->S

a --> b & c--> d
e & f--> g & h

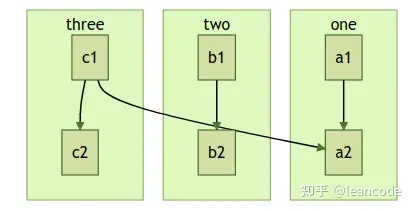
子图

ˋˋˋmermaid
graph TD
    c1 --> a2
    subgraph one
    a1-->a2
    end
    subgraph two
    b1-->b2
    end
    subgraph three
    c1-->c2
    end

ˋˋˋ

显示如下:

graph TD
    c1 --> a2
    subgraph one
    a1-->a2
    end
    subgraph two
    b1-->b2
    end
    subgraph three
    c1-->c2
    end

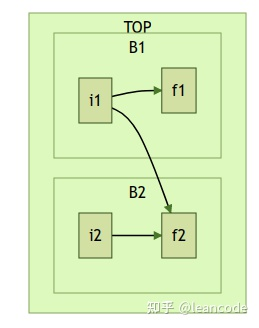
子图结构和方向

ˋˋˋmermaid
graph LR

  subgraph TOP
    direction TB
    subgraph B1
        direction RL
        i1 -->f1
    end
    subgraph B2
        direction BT
        i2 -->f2
    end
  end

    i1 --> f2

ˋˋˋ

显示如下:

graph LR

  subgraph TOP
    direction TB
    subgraph B1
        direction RL
        i1 -->f1
    end
    subgraph B2
        direction BT
        i2 -->f2
    end
  end

    i1 --> f2

自定义的CSS

ˋˋˋmermaid
graph LR
    id1(Start)-->id2(Stop)
    style id1 fill:#f9f,stroke:#f92,stroke-width:4px
    style id2 fill:#bbf,stroke:#f66,stroke-width:2px,color:#fff,stroke-dasharray: 5 5

    A:::someclass --> B
    classDef someclass fill:#f92;
ˋˋˋ

graph LR
    id1(Start)-->id2(Stop)
    style id1 fill:#f9f,stroke:#f92,stroke-width:4px
    style id2 fill:#bbf,stroke:#f66,stroke-width:2px,color:#fff,stroke-dasharray: 5 5

    A:::someclass --> B
    classDef someclass fill:#f92;

fill、stroke、stroke-width、color是CSS中的概念，分别表示填充、边框、边框宽度、字体颜色

ˋˋˋmermaid
graph TD
    B["fa:fa-twitter for peace"]
    B-->C[fa:fa-ban forbidden]
    B-->D(fa:fa-spinner);
    B-->E(A fa:fa-camera-retro perhaps?);
ˋˋˋ

graph TD
    B["fa:fa-twitter for peace"]
    B-->C[fa:fa-ban forbidden]
    B-->D(fa:fa-spinner);
    B-->E(A fa:fa-camera-retro perhaps?);

fa:fa-sppinner等以fa开始的是前端一套流行的图标库——fontawesome图标库

流程图实例


ˋˋˋmermaid
graph TD
    A[Start] --> B{Is it?};
    B -->|Yes| C[OK];
    C --> D[Rethink];
    D --> B;
    B ---->|No| E[End];
ˋˋˋ

显示如下:

graph TD
    A[Start] --> B{Is it?};
    B -->|Yes| C[OK];
    C --> D[Rethink];
    D --> B;
    B ---->|No| E[End];

文章写作要点

在描述文章信息时，理解tags、categories和keywords的不同是有助于有效组织和检索信息的。以下是对这三个概念的区分：

Tags（标签）

用途：标签通常用于指定与特定内容相关的词汇或短语，以便于搜索和组织。在Obsidian和其他知识库中，标签可以帮助你快速找到具有相同主题或属性的笔记。
特点：标签是灵活的，可以随意添加到笔记中。一个笔记可以有多个标签，同一个标签可以用于多个笔记。
实例：在Markdown文件中，你可能会看到类似#Tag1 #Tag2这样的标签。

Categories（分类）

用途：分类是一种更官方或结构化的组织方法。它们通常用于将内容分组到固定的、层次化的类别中。在一些内容管理系统（CMS）中，分类帮助定义笔记或文章的主要分组。
特点：分类通常比标签更正式和有限。一篇文章或笔记可能只属于一个或少数几个分类。
实例：例如，你可以有一个“技术”分类，下面有“编程语言”、“软件工具”等子分类。

Keywords（关键词）

用途：关键词是用来描述文档内容的词或短语，用于搜索引擎优化（SEO）或提高文档在搜索中的可见度。
特点：关键词通常是内容的精炼总结，有助于搜索算法理解和分类内容。它们可能不会直接显示在文档中，但在文档的元数据或头部信息中定义。
实例：在Markdown或HTML文档的头部，你可能会看到定义了关键词的元数据字段。

在实际应用中：

当你使用Obsidian、MGit或通过WebDAV同步坚果云时，你可能会利用这些概念来组织你的知识库或笔记：
- Tags：在Obsidian中，你可以给笔记添加标签来跟踪和链接相关主题。
- Categories：你可能会通过文件夹结构或特定字段来分类你的笔记，比如工作、学习、个人等。
- Keywords：在创建或编辑Markdown笔记时，你可能会考虑加入关键词来描述文档的主要内容，尤其是如果这些笔记将被发布到博客或网站上。

正确使用这些概念可以帮助你更有效地组织和检索你的笔记，使你的知识库更加有序和易于管理。

学习之路的起点

Hello world

VScode语法

Markdown语法

一级标题

二级标题

三级标题

加粗,斜体和删除线

Markdown Preview Enhanced 拓展功能

快捷键

列表

Markdown Preview Enhanced 拓展功能

引用和代码

Markdown Preview Enhanced 拓展功能

超链接和图片

剪贴板图片插入

表格

注释

数学公式支持

1.上标和下标

2.分式

3.根式

4.空格

5.累加累乘和积分

6.括号修饰

7.多行算式对齐

8.方程组

9.矩阵

10.特殊字符

11.公式编号与引用

12.零碎的用法

13.流程图教程

文章写作要点

Tags（标签）

Categories（分类）

Keywords（关键词）

在实际应用中：

发表回复取消回复

Hello world

VScode语法

Markdown语法

一级标题

二级标题

三级标题

加粗,斜体和删除线

Markdown Preview Enhanced 拓展功能

快捷键

列表

Markdown Preview Enhanced 拓展功能

引用和代码

Markdown Preview Enhanced 拓展功能

超链接和图片

剪贴板图片插入

表格

注释

数学公式支持

1.上标和下标

2.分式

3.根式

4.空格

5.累加累乘和积分

6.括号修饰

7.多行算式对齐

8.方程组

9.矩阵

10.特殊字符

11.公式编号与引用

12.零碎的用法

13.流程图教程

文章写作要点

Tags（标签）

Categories（分类）

Keywords（关键词）

在实际应用中：

发表回复 取消回复

发表回复取消回复